从最短路径算法Djikstra初谈
什么是Djikstra?
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
这是百度百科上的定义,用我们生活中的例子来讲
就相当于我们每天在地图上用的导航,导航可以帮我们在错综复杂的街道上,找到一条从出发地到达终点的最短路径
所以我们需要一个好的算法来干这事,而这种算法就叫做最短路算法(SSSP)
而其中Djikstra算法就是最短路算法中的一种(当然也是最简单的一种)
至于为什么叫Djikstra算法,因为Dijkstra算法是由一个叫Dijkstra的荷兰人发明的,故称此算法为Dijkstra算法。(怎么这么多废话)
好了,那现在进入正题
Dijkstra算法的工作原理?
因为这个算法是为了求出来在一系列限制条件下两个地方的最短路径,那么我们一般怎么找到从一个地方到另外一个地方的最短路呢?
对,我们首先得有一张地图才行啊
就拿我国庆去上海玩的经历来说吧
你现在刚从火车站出来搭地铁到人民广场这个下站了,天色已经很晚了,,但是你突然想走去黄浦江边的外滩去看风景
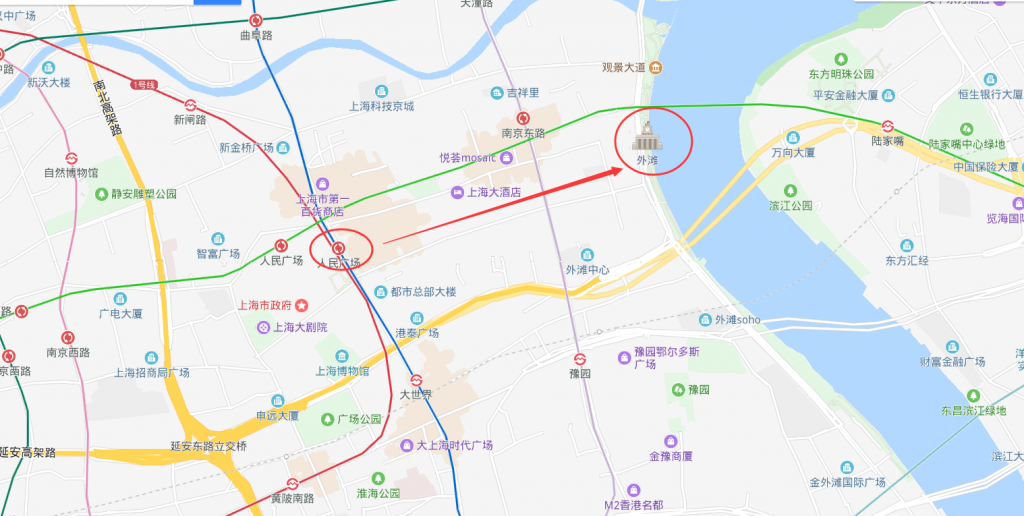
你可能要问,诶我为什么不继续坐地铁到那个南京东路下站然后再走去外滩啊,这样不是更近吗?
(然鹅不幸的是国庆的前几天南京东站的晚上基本上都是被封的)
所以你只能选择走去外滩,当然你不可能像红色箭头这样飞过去了,不然警察叔叔会罚你 $10^{10} RMB的,所以你只能找到合适的道路走过去,也就是说你只能走那些标记为“路”的地方
于是我们就可以把每一个路口或建筑看作一个点,有些点与另一些点之间有边连接,这个边其实就是马路,连结了两个地方。
当然,有些马路的车流量比较大,有些在比较小;于是有的马路通过需要花费的时间多,有的花费的时间少。我们把一条马路通过所需要花费的时间,称作这条边的权值。所有的点和边连在一起,就成为了一个图。
(没错如果你想直接从人民广场直接直接走到外滩几乎是不可能的,人流量可以把你窒息死)
图这种东西大概长这样:
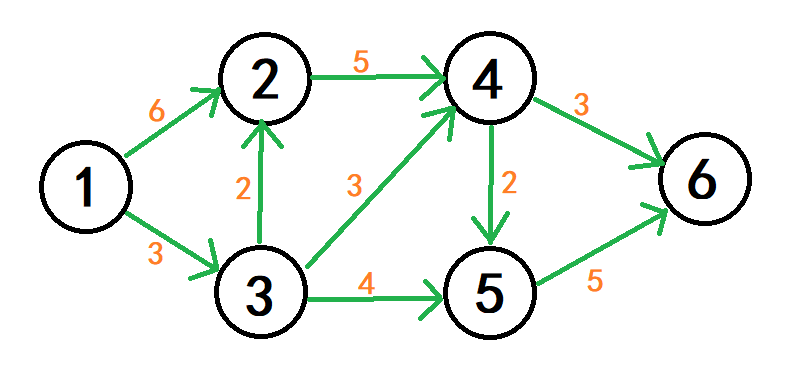
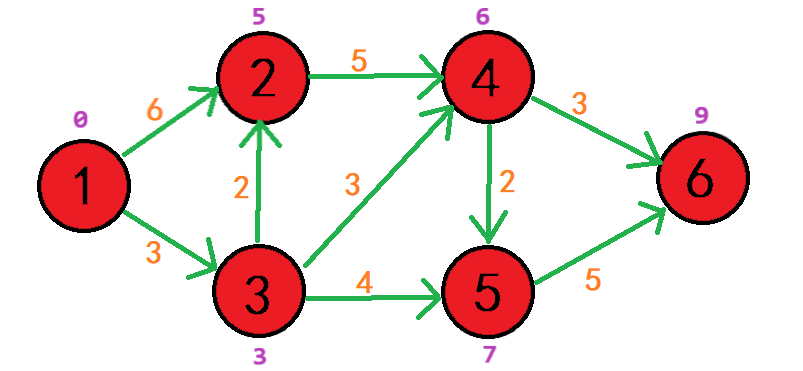
一个圆就是一个点,圆上的数字是点的序号,绿色的线是边,边旁边的橙色数字是边的权值。之所以加上箭头,是因为我们假设所有马路都是单行线(双向车道改成两条单向车道不就好了)。
具体的Dijikstra算法的证明过程在这里不再给出,具体的过程可以自行百度好了(其实是我的证明水平还8太行)
但是djikstra算法不适用于有负边权的图,在这里不再赘述
个人理解就是:dijkstra不能解决负权边是因为 dijkstra要求每个点被确定后st[j] = true,dist[j]就是最短距离了,之后就不能再被更新了(一锤子买卖),而如果有负权边的话,那已经确定的点的dist[j]不一定是最短了
对我的理解来说,Djikstra算法最直观的一个解释就是以起点开始寻找有没有其他中介点能够使起点到达其他顶点的距离能够变小
Djikstra算法的一个伪代码
bool vis[maxn] = {false};
void Djikstra(G, d[],s)
{
初始化
for(循环n次){
u = 使d[u]最小的还未访问的顶点的标号
vis[u] = true;//记下u已被访问
for(从u出发能到达的所有顶点v){
if(vis[v] == false && 以u为中介点使s到达顶点v的最短距离d[v]更优)
{
优化d[v];
}
}
}
}其中G为邻接矩阵,s为起点
vis[i] == true时表示顶点Vi已被访问,vis[i] == false时表示顶点Vi还未访问
d[]表示起点s到达顶点Vi的最短距离,初始化时除了起点的d[s]赋为0,其余的顶点都赋予一个很大的数(比如INT_MAX或者自己赋一个很大的INF)
(即相当于把除了起点与其他顶点的边权确认后,其余各个顶点之间的距离设为无穷大(即INF),这样可以保证后来各个点的最短距离d[i]都是从起点s得来的)
举一个简单的例子
拿一个简单的有向图来举例子吧
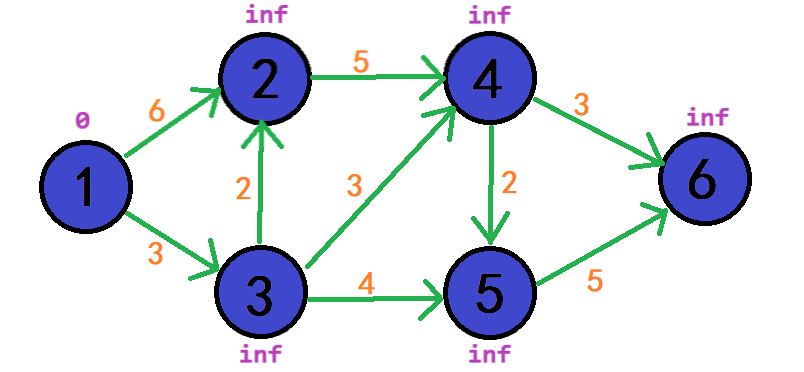
起点的d[s] = 0,其余点的d[i] = INF;
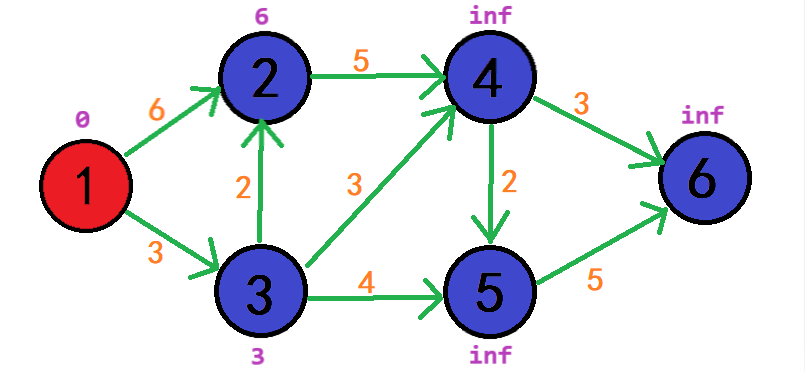
开始循环,起点1可以到达点3和点2
先把vis[1] = true;下次就不再循环到起点1
因为d[1] + weight[1][3] < d[3]所以更新d[3]
d[3] = d[1] + weight[1][3] = 3;
同理d[1] + weight[1][2] < d[2]所以更新d[2]
d[2] = d[1] + weight[1][2] = 6;

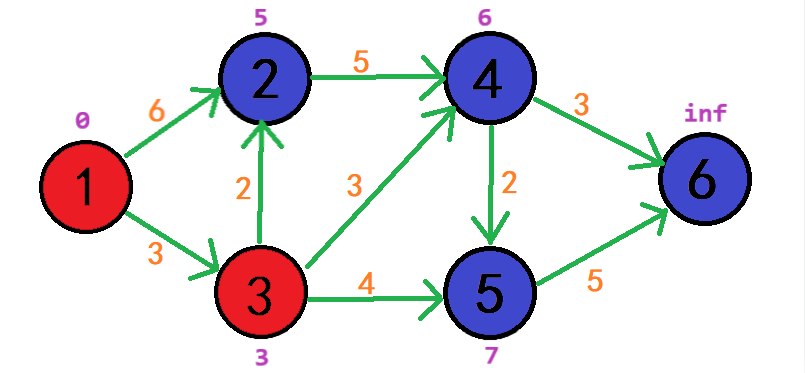
继续循环,寻找d[i]中最小的点(即离起点最近的)再开始计算
这时候d[3] = 3最小(因为d[1]已经被标记过了不再访问)
此时就以点3为中介点,看起点以它为中介点到达另外点的距离能不能变短
标记vis[3] = true;
此时d[3] + weight[3][2] < d[2]; 3 + 2 < 6 (即从1->3->2的距离比1->2的离更小)
所以更新d[2] = d[3] + weight[3][2] = 5;
又以点3中介点可以到达点4
d[3] + weight[3][4] < d[4];
3 + 3 < INF
此时更新d[4] = d[3] + weight[3][4] = 6;
同理以点3中介点可以到达点5
d[3] + weight[3][5] < d[5];
3 + 4 < INF
此时更新d[5] = d[3] + weight[3][5] = 7;
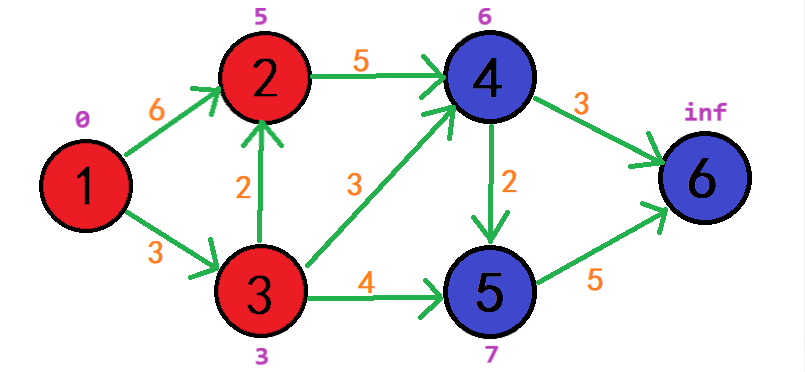
此时还能访问的d[2] = 5,d[4] = 6,d[5] = 7,d[6] = INF;
然后继续循环发现d[2]最小,于是再以2为中介点进行寻找
vis[2] = true;
d[2] + weight[2][4] > d[4];
5 + 5 > 6
此时不更新,由于2只能到达4所以结束循环

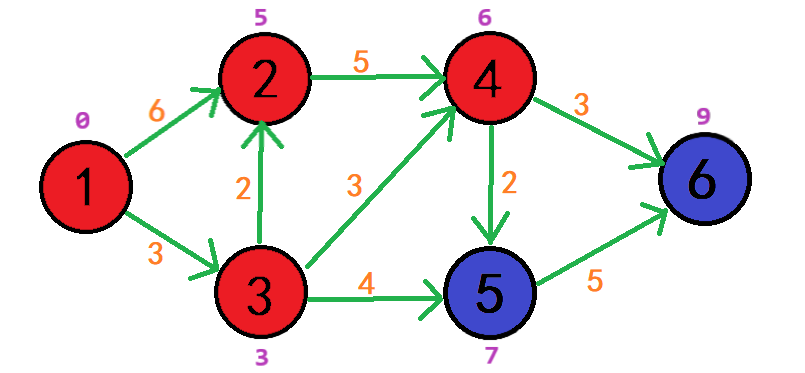
此时还能访问的d[4] = 6,d[5] = 7,d[6] = INF;
于是以点4为中介点进行循环
vis[4] = true;
由于点4可以到达点5和点6
d[4] + weight[4][5] > d[5]
6 + 2 > 7
不更新,继续循环
d[4] + weight[4][6] < d[6]
6 + 3 < INF
所以d[6] = d[4] + weight[4][6] = 9;
然后结束循环
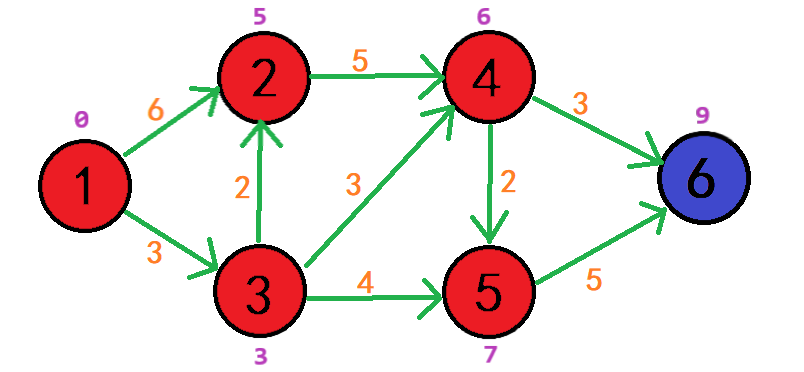
此时还能访问的d[5] = 7,d[6] = 9;
以点5为中介点进行循环
vis[5] = true;
由于点5可以到达点6
d[5] + weight[5][6] > d[6]
7 + 5 > 9
所以不更新,结束循环
此时还能访问的d[6] = 9;
vis[6] = true;
最后发现除了6自己以外其他点都已访问过,所以结束循环
最后的结果就是
d[1] = 0
d[2] = 5
d[3] = 3
d[4] = 6
d[5] = 7
d[6] = 9
如果您还看不懂请戳这里。
具体实现的代码,以邻接矩阵作为举例
这里是以PAT1003为举例
#include<bits/stdc++.h>
using namespace std;
const int maxn = 510;//最大的城市数
//N表示一共有N座城市 M表示一共有M条道路 C1 C2分别表示起点和终点
int N,M,C1,C2;
bool vis[maxn] = {false};//定义一个数组来判断城市是否被访问
int G[maxn][maxn];//表示城市与城市之间的距离
int pre[maxn];//存储前驱结点
int d[maxn];//记录最短距离,d[u]表示从起点s到达顶点u的最短距离
int weight[maxn];//每个点的权值
int w[maxn];//记录起点到每个点的最大权值
int num[maxn];//num[u]表示起点s到达顶点u的最短路径条数
void dijkstra(int s)//s表示起点
{
fill(d,d+N,INT_MAX);//把所有点的距离都抹掉
d[s] = 0;//把起点的最短距离设置为0
w[s] = weight[s];//起点开始的权值即为起点的权值
num[s] = 1;
for(int i = 0;i < N;i++){ //循环n次
int u = -1,MIN = INT_MAX;//u设置为-1是为了方便当找不到可以连接的点时方便判断,MIN存放最小的d[u],
for(int j = 0;j < N;j++)
{
//找到未访问顶点中d[]最小的顶点,因为从起点开始更新了后面的d[u],然后下次循环就要从这个点寻找能到达顶点中距离最小的那个点
if(d[j] < MIN && vis[j] == false)
{
u = j;//找到跟起点相距最短的那个点
MIN = d[j];//更新最短的距离
}
}
if(u == -1) return ;//如果找不到小于INT_MAX的d[],意味着剩下的顶点和起点s不连通
vis[u] = true;//标记为已访问
for(int v = 0;v < N;v++)
{ //如果u能到达v 且 v未访问 -> 则以u为中介点到达v可以使d[v]更优
if(G[u][v] != 0 && vis[v] == false )
{
//当以u为中介点的时候能使d[v]变小
if(d[u] + G[u][v] < d[v] )
{
d[v] = d[u] + G[u][v];//覆盖d[v]
w[v] = w[u] + weight[v];//更新w[v]
num[v] = num[u];//覆盖num[v]
}
else if(d[u] + G[u][v] == d[v])//找到一条相同长度的路径后
{
if(w[v] < w[u] + weight[v])//如果这条路径的点权之和更大
{
w[v] = w[u] + weight[v];//更新
}
num[v] += num[u];//有相同路径长度,则相加num[u],因为当d[u] + G[u][v] < d[v]时候已经算出一个num[v]是符合条件的
} //那么当d[u] + G[u][v] == d[v]时之前d[u] + G[u][v] < d[v]算的num[v]仍然符合条件,则继续加上现在相等时候的num[u]
}
}
}
}分析算法的复杂度?
从复杂度来看,主要是外层循环O(V)与内层循环(寻找最小的d[u]需要O(V)、枚举v需要O(V))产生的,总复杂度为O(V*(V+V)) = O(V^2).
但其实Djikstra算法是可以优化到O(nlogn + m)的级别的
为什么?
因为必须把每个点都标记为已访问(即vis[i] = true),所以外层循环的O(V)时间是无法避免的
但是寻找最小的d[u]的过程可以不必要一个一个重新循环去寻找最小的那个的d[u]
可以通过堆优化来降低复杂度,最简单的做法就是直接用STL中的优先队列priority_queue(STL依赖症)
看了上面的代码你可能已经发现了一个问题,那就是如果题目除了最短路径还有其他的要求怎么办?
比如PAT1003里面就要求找到从起点到终点的最短路径的条数以及最短路径的数目之和
即最短的路径可能不止一条
于是有三种主要的方式来进行考察
①新增边权,即以新增的边权花费为例
cost[u][v]表示从u -> v的花费,并增加一个数组c[],令起点s到达顶点u的最少花费为c[u]同理初始化的时候c[s] = 0,其余均为INF
这样就可以在d[u] + G[u][v] < d[v]时更新d[v]和c[v]
而当d[u] + G[u][v] == d[v]时且c[u] + cost[u][v] < c[v]时更新c[v]
(即可以是s到v的最少花费更优时更新c[v])
样例代码:
for(int v = 0;v < n;v++){
//如果v未访问 && u能到达v
if(vis[v] == false && G[u][v] != INF){
if(d[u] + G[u][v] < d[v]){
d[v] = d[u] + G[u][v];
c[v] = c[u] + cost[u][v];
}
else if(d[u] + G[u][v] == d[v] && c[v] > c[u] + cost[u][v]){
c[v] = c[u] + cost[u][v];
}
}
}②新增点权,即以新增的点权代表城市能收集到的物资为例,用weight[u]表示城市u中的物资数目,并新增一个数组w[],即从起点s到达顶点u可以收集到的最大的物资为w[u],初始化的时候w[s] = weight[s],其余均为0,这样就可以在d[u] + G[u][v] < d[v]时更新d[v]和w[v] 而当d[u] + G[u][v] == d[v]时且w[u] + weight[u][v] > w[v]时更新w[v]
(即可以使s到v的最大物资更优)
代码与上面类似不再给出
③求最短路径条数,只需要增加一个数组num[],令从起点s到达顶点u的最短路径条数为num[u],初始化时num[s]为1,其余num[u]均为0
这样可以使当d[u] + G[u][v] < d[v]使num[v]继承num[u]
而当d[u] + G[u][v] == d[v]时将num[u]加到num[v]上
代码如下
for(int v = 0;v < n;v++){
//如果v未访问 && u能到达v
if(vis[v] == false && G[u][v] != INF){
if(d[u] + G[u][v] < d[v]){
d[v] = d[u] + G[u][v];
num[v] = num[u];
}
else if(d[u] + G[u][v] == d[v]){
num[v] += num[u];
}
}
}鉴于时间关系暂时就先总结这么多,Dijikstra算法其实能扩展的东西还有很多,比如如果题目要求具体的最短路径的话还要另外增加一个记录前驱结点的数组之类的东西,等以后有时间我再来补齐吧!


