题目
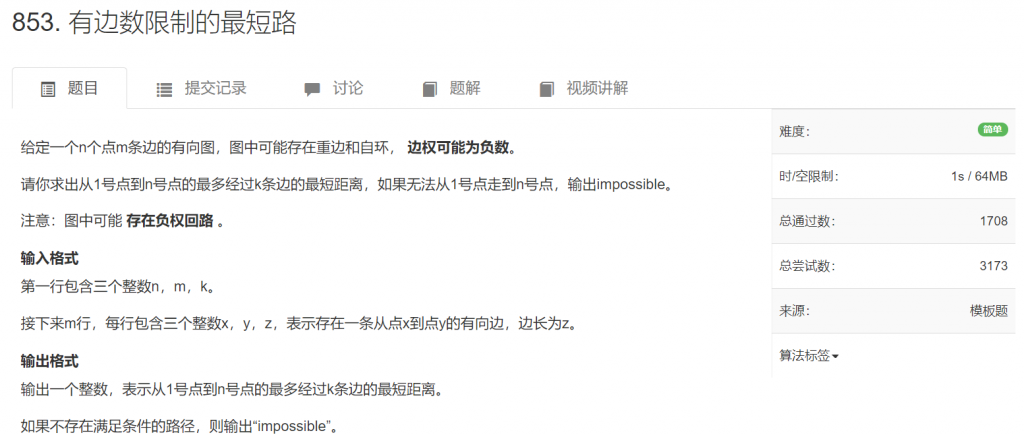
输入输出
分析思路
dijkstra算法不能处理有负权边的情况
Bellman-Ford算法适用于带负环的图,如果题目限制了最短路经过的边的个数,如上图的代码,那么有负环也无所谓了,因为限制k次导致我们不能无限的经过负环
实现思路:
for(循环n次)
for(循环所有边a,b,w)
dist[b] = min(dist[b],backup[a]+w)
//其中所有边就可以直接用一个结构体数组来存储,不一定需要邻接表,只要能遍历到所有边就可以了为什么用backup[N]数组来存放上一个的结果


如图所示,如果题目要求k = 1,那么我们从1到3只能选择下面一条路径去求
如果不用backup数组来存放上一个的话
那么
d[1] = 0
d[2] = min(d[1]+1,d[2]) = 1
此时再继续循环d[3]= min(d[2]+1,d[2]) = 2
此时d[3]就是用上一个已经更新了的2来继续更新的
此时则发生串联
那么我们只调用上一个的backup数组
d[1] = 0;
backup[1] = 0,backup[2] = INF,backup[3] = INF;
d[2] = min(d[2],backup[1]+1) = 1//1--2(1)
d[3] = min(d[3],backup[2]+1) = INF//2--3(1)
d[3] = min(d[3],backup[1]+3) = 3//1--3(3)
时间复杂度为O(nm)

注意点
1.为什么是d[n] > 0x3f3f3f3f/2?
因为存在负权边,那么虽然n也是正无穷,但是经过负权边可能会把n的正无穷减小一点,但是也不会减太多,最多减500*10000,所以写成d[n] > 0x3f3f3f3f/2即可判断
2.memset函数是以字节为单位赋值的,每个int包含4个字节,所以memset完之后所有数会变成0x3f3f3f3f
代码如下
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 510,M = 10010;
int n,m,k;
int d[N],backup[N];
struct Edge{
int a,b,w;
}edges[M];
int bellman_ford(int s)
{
memset(d,0x3f,sizeof d);
d[s] = 0;
for(int i = 0;i < k;i++)
{
memcpy(backup,d,sizeof d);
for(int j = 0;j < m;j++)
{
int a = edges[j].a,b = edges[j].b,w = edges[j].w;
d[b] = min(d[b],backup[a] + w);
}
}
if(d[n] > 0x3f3f3f3f/2) return -1;
return d[n];
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
int i = 0;
for(int i = 0;i < m;i++){
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
edges[i] = {a,b,w};
}
int t = bellman_ford(1);
if(t == -1) puts("impossible");
else printf("%d\n",t);
return 0;
} SPFA算法
题目
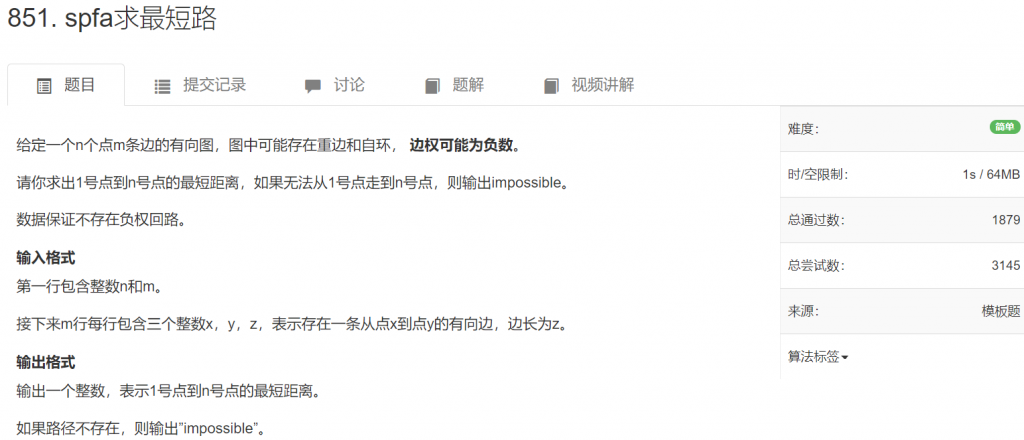
输入输出
分析思路
SPFA算法是bellman-ford算法的优化
在bellman-ford算法中,他要遍历所有边来进行更新,但是每一次迭代不一定每一条边都需要更新
dist[b] = min(dist[b],dist[a]+w)
那么SPFA可以对其进行优化
dist[b]如果想变小的话,那么一定是dist[a]变小了
如果dist[a]不变,那么dist[b]也一定不变
那么我们每次就可以用一个队列(堆、优先队列,但是一般来说用队列就可以了)进行存储,队里面就存放的就是所有变小的结点,只要队列里面不空,就取出队头t,更新t的所有出边,如果更新成功,就把b加入队列,如果队列里面已经有b了,就不用再存放进队列里面了
它的基本思路就是我更新过谁,我就再拿谁去更新别人,一个点如果没有被更新过,那么它就没有必要去更新别人,只有前面的点变小了,后面的点才会跟着变小
我的理解就是,它这个点变小了,他肯定会影响更多的点,所以就需要放入队列里面进行操作
注意点
1.spfa只会更新所有能从起点走到的点,所以如果无解,那么起点就走不到终点,那么终点的距离就是0x3f3f3f3f
代码如下
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
//用vector建图的写法
const int N = 1e5+10;
int d[N];//d[i]表示从起点到i的距离
int vis[N];//i是否在队列中
int n,m;//n个点m条边
struct node{
int to,w;//to代表终点,w代表a->b的边权
};
vector<node>G[N];//相当于拉链法,G[i]插入i连接的各个结点
int main()
{
scanf("%d %d",&n,&m);
memset(d,0x3f,sizeof d);
for(int i = 0;i < m;i++)
{
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
G[a].push_back({b,c});
}
d[1] = 0;//1号点初始化为0
queue q;
vis[1] = true;//1号点在队列中
q.push(1);
while(q.size())
{
int t = q.front();
q.pop();
vis[t] = false;
for(int i = 0;i < G[t].size();i++)
{
int b = G[t][i].to;//t相连的点为b
int dist = G[t][i].w;//t到b的距离为dist
if(d[b] > d[t] + dist)//如果从起点到t再到b的距离比起点到b的距离要短的话
{
d[b] = d[t] + dist;//更新最短距离
if(!vis[b])//如果b不在队列里面的话
{
q.push(b);
vis[b] = true;
}
}
}
}
if(d[n] == 0x3f3f3f3f) puts("impossible");
else printf("%d",d[n]);
return 0;
} SPFA判断负环
题目
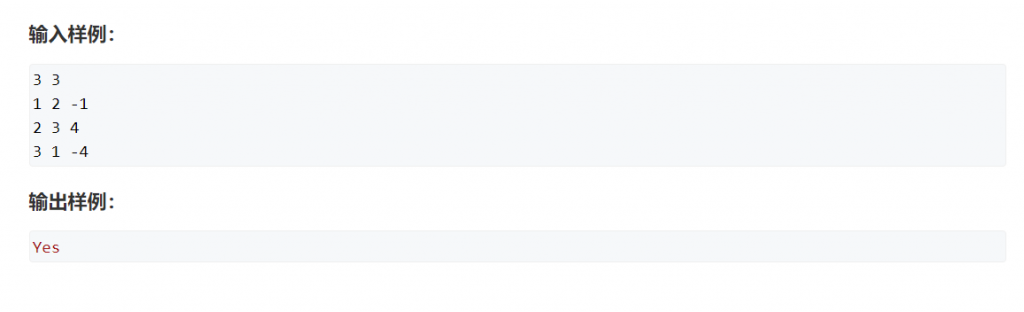
输入输出
分析思路
在SPFA算法中dist[x]表示从起点s到x的最短距离
那么我们可以用一个cnt[N]数组来存放,表示边数
dist[x] = dist[t] + w[i]
cnt[x] = cnt[t] + 1
1----------t——x
| |
---------------因为上面表示从1到t再到x的路径比下面的要短
那么从1到t再到x的边数就是从1到t的边数再+1
即cnt[x] = cnt[t] + 1
此时如果cnt[x]>=n的话,意味着从1到x至少经过了n条边,经过了n条边如果没有环的话就意味着有n+1个点,但是我们题目只有n个点,说明最短路径中存在环,这个环一定是负权的,因为如果是正权的,那经过这个环路径会变大,那我肯定不会经过这个环
所以SPFA算法可以用来判断是否有负环
注意点
1.有负环的话相当于某些点到起点的距离为负无穷,然后SPFA算法是正确的,且初始时这些点的距离为0,0大于负无穷,所以一定会把这些距离为负无穷的点不断更新,所以不需要把d数组赋值为正无穷
代码如下
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int h[N],e[N],ne[N],d[N],w[N],idx,cnt[N];
bool vis[N];//vis[i]是判断是否存入过队列中
int n,m;
void add(int a,int b,int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
int spfa()
{
queueq;
for(int i = 1;i <= n;i++)
{
vis[i] = true;
q.push(i);
}
while(!q.empty())
{
int t = q.front();
q.pop();
vis[t] = false;
for(int i = h[t];i != -1;i = ne[i])
{
int j = e[i];
if(d[j] > d[t] + w[i])
{
d[j] = d[t] + w[i];
cnt[j] = cnt[t] + 1;
if(cnt[j] >= n) return 1;
if(!vis[j])
{
q.push(j);
vis[j] = true;
}
}
}
}
return 0;
}
int main()
{
scanf("%d %d",&n,&m);
memset(h,-1,sizeof h);
//memset(d,0x3f,sizeof d);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
int t = spfa();
if(t) puts("Yes");
else puts("No");
return 0;
} 

