继续完成这个星期的存货

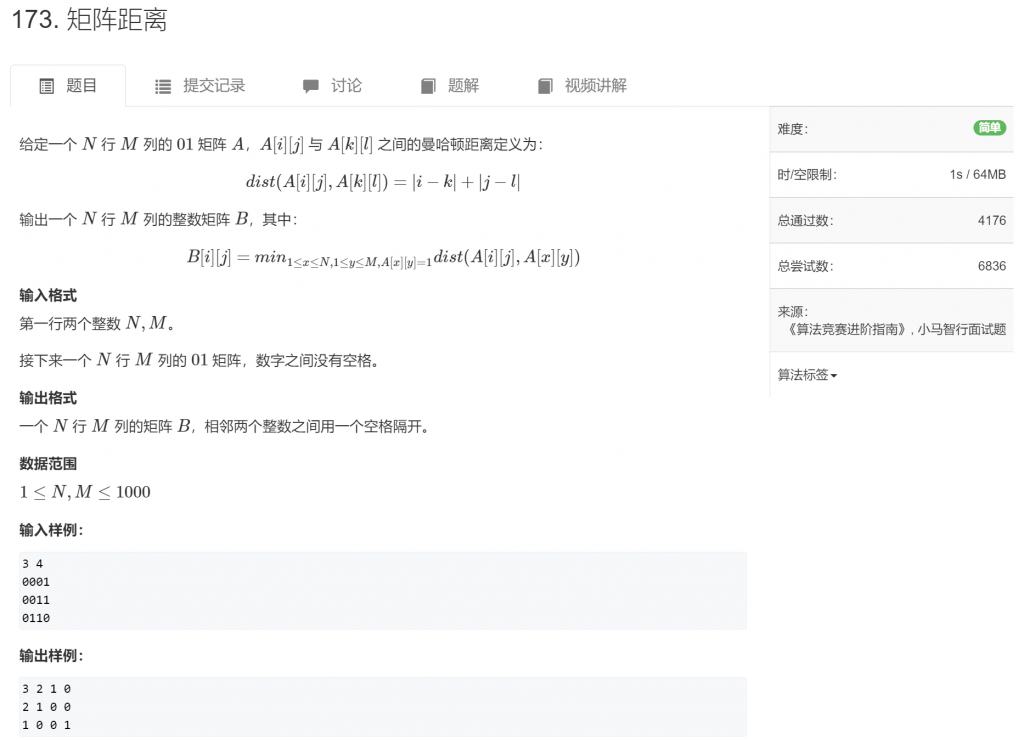
• 分析

• 自己的分析
  • 本题可以看作有多个起始状态的floodfill,把矩阵A中每一个1都看作起点
  • 整个矩阵都可以通行，对于每个位置，从任何一个起点出发都可以的情况下
  • 求到达该位置所需要的最小步数
  • 这种多种等价起始状态的问题，只需要BFS开始之前把所有的起始状态都插入队列中
  • 比如先把A插入队列中，然后拓展离A最近的一层的所有的点，然后插入队尾
  • 这个离A最近的一层的点，被A拓展过之后，就不会再被其他点所拓展
  • 因为我们的前提就是所有起始状态都是等价的
  • 而且在队列之中，永远都是队列前面的点所被拓展的距离比队列后要小(这样就跟djisktra里面的优先队列类似)
  • 而且被队列前面所拓展的点不会再被队列后的点所拓展

#include <iostream>
#include <cstring>

using namespace std;

/**
 * 查看题解：https://www.acwing.com/solution/content/40236/
 * 本题可以看作有多个起始状态的floodfill,把矩阵A中每一个1都看作起点
 * 整个矩阵都可以通行，对于每个位置，从任何一个起点出发都可以的情况下
 * 求到达该位置所需要的最小步数
 * 这种多种等价起始状态的问题，只需要BFS开始之前把所有的起始状态都插入队列中
 * 比如先把A插入队列中，然后拓展离A最近的一层的所有的点，然后插入队尾
 * 这个离A最近的一层的点，被A拓展过之后，就不会再被其他点所拓展
 * 因为我们的前提就是所有起始状态都是等价的
 * 而且在队列之中，永远都是队列前面的点所被拓展的距离比队列后要小
 * 而且被队列前面所拓展的点不会再被队列后的点所拓展
 */ 
#define x first
#define y second

typedef pair<int,int> PII;

const int N = 1010,M = N*N;
int n,m;
int dist[N][N];
char g[N][N];
int hh = 0,tt = -1;
PII q[M];
int dx[4] = {1,0,-1,0};
int dy[4] = {0,-1,0,1};

int main()
{
    scanf("%d %d",&n,&m);
    memset(dist,-1,sizeof dist);//把所有的值全部初始化成-1，代表没走过
    for(int i = 0;i < n;i++) scanf("%s",g[i]);
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j < m;j++)
        {
            if(g[i][j] == '1')
            {
                dist[i][j] = 0;
                q[++tt] = {i,j};
            }
        }
    }
    
    while(hh <= tt)
    {
        PII t = q[hh++];
        for(int k = 0;k < 4;k++)
        {
            int sx = t.x + dx[k],sy = t.y + dy[k];
            if(sx < 0 || sx >= n || sy < 0 || sy >= m) continue;
            if(dist[sx][sy] == -1)//如果还尚未走过的话
            {
                dist[sx][sy] = dist[t.x][t.y] + 1;
                q[++tt] = {sx,sy};
            }
        }
    }

    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j < m;j++)
        {
            printf("%d ",dist[i][j]);
        }
        printf("\n");
    }
    
    return 0;
}